Brücken ist ein Brücken-Rätsel, das aus einer rechteckigen Anordnung von Kreisen mit Zahlen besteht. Die Kreise sollen Inseln darstellen, und die Zahlen geben an, wie viele Brücken mit einer Insel verbunden sind. Ziel ist es, alle Inseln waagrecht und senkrecht mit Brücken zu verbinden, sodass die vorgegebenen Zahlen mit den Brücken übereinstimmen. Ausserdem dürfen nur ein oder zwei Brücken in ein- und dieselbe Richtung führen, und es muss ein durchgehender Pfad entstehen, der alle Inseln miteinander verbindet. Die Brücken dürfen keine Inseln oder andere Brücken kreuzen.

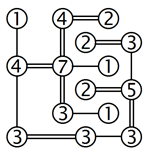
Techniken für den Rätselstart
Bei den meisten Brücken-Rätseln, besonders bei den sehr leichten, sind die ersten Schritte auf den ersten Blick klar. Das ist zum Beispiel dann der Fall, wenn eine Insel die grösstmögliche Zahl an Brücken fordert. In einigen der folgenden Beispiele gibt es Inseln ohne Zahlen, was bedeutet, dass die Zahlen an diesen Stellen für die Lösetechniken in diesem Stadium nicht von Bedeutung sind. Hier werden einige der Starttechniken vorgestellt:
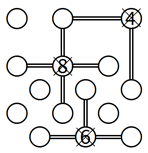
1. Inseln mit einer 4 in der Ecke, einer 6 an der Seite und einer 8 in der Mitte:
Eine Insel in einer Ecke kann nicht mehr als zwei Nachbarn haben, und die Anzahl der Brücken für jeden Nachbarn kann nicht höher als zwei sein. Das heisst, dass die Insel mit der 4 in der oberen linken Ecke mit jeweils zwei Brücken mit ihren beiden Nachbarinseln verbunden ist. Genauso muss die Insel mit der 6 am unteren Rand mit seinen drei Nachbarn durch jeweils zwei Brücken verbunden sein, und die Insel in der Mitte des Rätsels mit der 8 muss durch jeweils zwei Brücken mit ihren vier Nachbarinseln verbunden werden. In allen Fällen ist die grösstmögliche Zahl an Brücken eingezeichnet, sodass diese Inseln mit einem X markiert werden können.

Grundtechniken
Die Grundtechniken kommen dann zur Anwendung, wenn wir nicht alle Brücken eindeutig zuordnen, aber entscheiden können, in welcher Richtung eine oder mehrere Brücken platziert werden müssen. Hier einige Beispiele für die Grundtechniken:
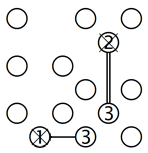
1. Inseln mit einem einzigen Nachbarn:
Die Insel mit der 1 unten hat nur einen Nachbarn auf der rechten Seite. Wir müssen diese beiden Inseln also mit einer Brücke verbinden. Genauso hat die 2 oben rechts nur einen Nachbarn, mit dem sie also durch zwei Brücken verbunden werden muss. In beiden Fällen sind alle Brücken eingezeichnet, sodass beide Inseln mit einem X markiert werden können. Beachten Sie, dass eine Insel, die nur einen Nachbarn hat, niemals eine 3 oder eine höhere Zahl beinhalten kann, denn das würde die Brücken-Regeln verletzen.

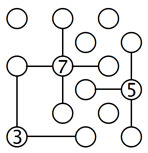
2. Inseln mit einer 3 in der Ecke, einer 5 an der Seite und einer 7 in der Mitte:
Eine Insel in einer Ecke mit einer 3 muss zwei Nachbarn haben, wobei sie mit dem einen durch eine und mit dem anderen durch zwei Brücken verbunden sein muss. Auch wenn wir noch nicht genau wissen, wie genau sich die Brücken aufteilen, so wissen wir sicher, dass die 3 in der unteren linken Ecke unseres Beispiels mit beiden Nachbarn durch eine Brücke verbunden ist. Genauso verhält es sich mit der 5 an der Seite, die mit jedem ihrer drei Nachbarn auf jeden Fall durch eine Brücke verbunden ist, und mit der 7, die mit jedem ihrer vier Nachbarn durch mindestens eine Brücke verbunden werden kann.

3. Besondere Fälle von 3 in der Ecke, 5 an der Seite und 7 in der Mitte:
Wenn eine 3 in einer Ecke einen Nachbarn hat, der eine 1 enthält, dann ist dieser Fall klar und alle drei Brücken können eingezeichnet werden. Genau das Gleiche gilt für eine 5 an der Seite und eine 7 in der Mitte, die Nachbarn mit einer 1 haben.

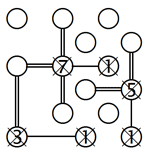
4. Der besondere Fall einer 4 an der Seite:
In diesem Beispiel sehen wir eine Insel mit einer 4 in der vorletzten Reihe. Auch wenn die 4 nicht an der Seite steht, können wir sie als solche behandeln, da sie nur drei Nachbarn hat. Weil nicht mehr als zwei Brücken in einer Richtung erlaubt sind, sind alle Bedingungen erfüllt und die vier Brücken können eingezeichnet werden: Zwei Brücken zu der darüberliegenden Insel und jeweils eine zu den beiden Inseln daneben.

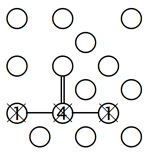
5. Der besondere Fall einer 6 in der Mitte:
Nehmen wir an, dass die Insel mit der 6 mit der Insel mit der 1 verbunden ist. Dann würden fünf Brücken übrig bleiben, was wiederum bedeutet, dass sie durch mindestens eine Brücke mit A, B und C verbunden ist. Lassen Sie uns jetzt annehmen, dass es keine Verbindung zur 1 gibt. In diesem Fall wäre die 6 mit jeweils zwei Brücken mit A, B und C verbunden. Also, egal, ob es eine Verbindung zwischen der 6 und der 1 gibt, ist die 6 auf jeden Fall durch mindestens jeweils eine Brücke mit A, B und C verbunden.

Isolierungstechniken
Eine der Brücken-Regeln fordert, dass ein durchgehender Pfad entsteht, der alle Inseln miteinander verbindet. Diese Regel, die selbst bei den einfachsten Brücken-Rätseln von Bedeutung ist, führt zu interessanten logischen Situationen, ohne die das Rätsel nicht gelöst werden kann. Hier einige Situationen, in denen die Isolierungstechniken zur Anwendung kommen:
1. Isolierung einer Zweier-Inselgruppe:
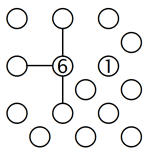
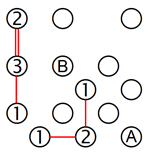
Schauen wir uns die 1 in der rechten Spalte an. Wenn wir sie mit der darüberliegenden 1 verbinden, bilden die beiden Inseln einen isolierten Bereich, was gemäss den Brücken-Regeln nicht erlaubt ist. Die einzige andere Möglichkeit ist, sie mit A zu verbinden. Genau dasselbe gilt für die 2 links unten, von der mindestens eine Brücke zu B führen muss, damit kein isolierter Bereich entsteht.
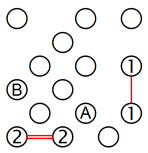
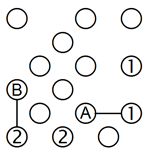
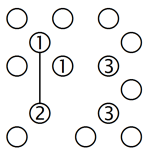
2. Isolierung einer Dreier-Inselgruppe:
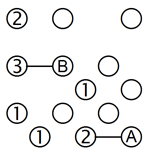
Diese Technik kann auch auf drei Inseln erweitert werden. Die 2 am unteren Rand kann nicht mit den beiden Einsen verbunden werden, wie im linken Gitter dargestellt, denn dann wären diese drei Inseln isoliert. Das heisst, es muss mindestens eine Brücke zu A führen. Dasselbe gilt für die 3 in der Spalte ganz links. Wenn man sie ausschliesslich mit der 2 und der 1 verbindet, entsteht eine isolierte Dreiergruppe, also muss es mindestens eine Verbindung zu B geben.
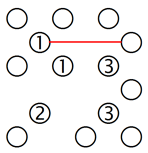
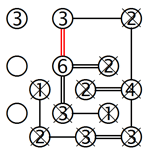
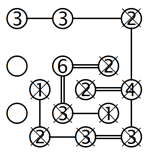
3. Grössere isolierte Gruppen:
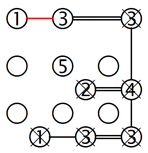
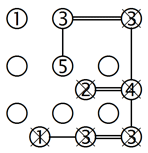
Manchmal passiert es, dass noch grössere Inselgruppen isoliert werden und so logische Situationen entstehen, die schwieriger und deshalb interessanter zu lösen sind. Betrachten wir das Beispiel im linken Gitter. Wir sehen eine Gruppe von sieben Inseln, von denen sechs komplett sind und nur bei der 3 in der obersten Reihe eine Brücke fehlt. Wenn wir sie mit der 1 in der oberen linken Ecke verbinden, wie die rote Linie zeigt, führt das zu einer isolierten Gruppe. Also muss diese Insel mit der 5 verbunden werden, wie im rechten Gitter zu sehen ist.
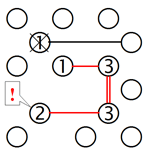
4. Isolierung durch aneinandergrenzende Gruppen:
Im linken Gitter haben wir zwei Inselgruppen. Eine mit vier Inseln, bei der alle Inseln verbunden sind ausser der Insel mit der 6, und die andere mit acht Inseln, die alle verbunden sind, ausser der Insel mit der 3. In beiden Gruppen fehlen bei den unvollständigen Inseln zwei Brücken. Wenn wir jetzt die 6 und die 3 miteinander verbinden, wie die rote Linie zeigt, enden wir mit einer grossen isolierten Gruppe. Also können wir davon ausgehen, dass mindestens eine Brücke zu der 3 oben links führt, wie Sie im rechten Gitter sehen können.
Fortgeschrittene Techniken
Mit den bis hierher beschriebenen Techniken wird es nicht möglich sein, schwere Rätsel zu lösen. Für diese braucht man fortgeschrittene Techniken, um zahlreiche spezielle und interessante logische Situationen herauszuarbeiten. Bei vielen fortgeschrittenen Techniken blickt man nach vorne, stellt Vermutungen an und schaut ein oder zwei Schritte weiter nach möglichen Konflikten. Auch wenn die Ergebnisse, die man durch fortgeschrittene Techniken erzielt, manchmal denen früherer Lösungswege ähneln, gibt es einen grossen Unterschied, denn der Rätsellöser muss nach vorne schauen, um logische Konflikte oder Widersprüche zu entdecken. Hier werden einige Beispiele für solche Lösungstechniken vorgestellt. Sie werden selbst noch viele weitere entwickeln, wenn Sie ein Brücken-Rätsel lösen:
1. Durch Blockieren einer Brücke eine Gruppe isolieren:
Wenn wir annehmen, dass im linken Gitter keine Brücke in die Richtung führt, wo das rote Kreuz steht, dann müssen die fünf Inseln so verbunden werden, wie im mittleren Gitter zu sehen ist, was zu einer isolierten Gruppe führt.
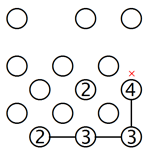
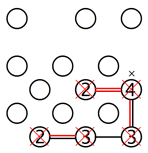
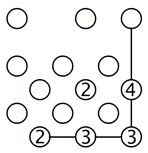
2. Eine Gruppe isolieren, indem man eine Brücke baut:
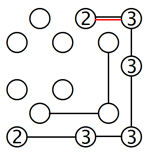
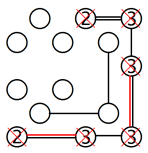
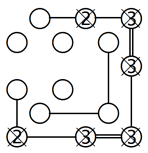
Schauen wir uns die obere Reihe im linken Beispiel an. Wenn wir annehmen, dass die 2 mit der Insel rechts verbunden ist, wird eine Gruppe von sechs Inseln isoliert, wie das Gitter in der Mitte zeigt. Aus diesem Grund muss diese Insel so verbunden werden, wie in dem rechten Beispiel zu sehen ist. Genauso muss auch die Insel in der unteren linken Ecke mit der Insel darüber verbunden werden.
3. Eine Insel mit Brücken isolieren:
Betrachten wir die 2 im linken Gitter. Wenn wir annehmen, dass es keine Brücke in die Richtung gibt, wo sich das rote X befindet, muss die 2 so verbunden werden, wie es das Beispiel in der Mitte zeigt. Das führt aber dazu, dass die Insel mit der 1 isoliert wird, da die einzige andere Insel, mit der sie verbunden werden könnte, schon eine Verbindung hat. Also muss es mindestens eine Brücke geben, die nach unten führt, was im Gitter rechts dargestellt ist.
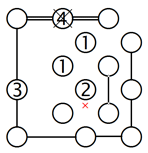
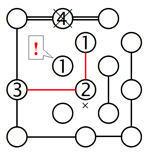
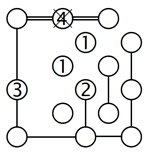
4. Verbindungskonflikte heraufbeschwören:
Die Insel mit der 1 in der zweiten Reihe kann in zwei Richtungen verbunden werden. Nehmen wir an, sie ist mit der Insel rechts verbunden, wie im Beispiel links zu sehen ist. Das würde zu einer isolierten Vierergruppe führen, wie das Gitter in der Mitte zeigt. Die Insel mit der 2 hat immer noch eine mögliche Verbindung frei, die einen Konflikt verursacht! Also muss die 1 in der zweiten Reihe mit der Insel unten verbunden werden, was im linken Gitter veranschaulicht wird.