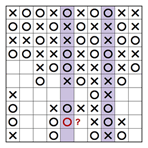
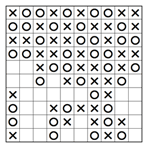
Binoxxo ist ein Singleplayer-Rätsel, das an 3-Gewinnt erinnert, ein Spiel, das viele von uns als Kinder geliebt haben. Jedes Rätsel besteht aus einem Gitter mit den Buchstaben X und O an verschiedenen Stellen. Ziel ist es, die übrigen Kästchen so mit X und O zu füllen, dass in jeder Spalte oder Reihe niemals mehr als zwei aufeinanderfolgende X oder O vorkommen und dass alle Reihen und Spalten einzigartig sind. In dem Beispiel unten haben wir ein Binoxxo-Rätsel (6×6) mit sechs Reihen und sechs Spalten. Wir müssen jetzt X und O gemäss den Regeln in die übrigen Kästchen einsetzen … aber wie?

Basistechniken
Binoxxo-Rätsel beginnen mit einigen sehr einfachen Schritten, die auf der 1. Regel basieren, in der es heisst, dass nicht mehr als zwei aufeinanderfolgende X oder O in einer Reihe oder Spalte auftauchen dürfen. Es folgen weitere einfache Schritte gemäss der 2. Regel, nach der in einer Reihe oder Spalte die Anzahl der X und O gleich sein muss, sowie gemäss der 3. Regel, die fordert, dass keine Reihe oder Spalte einer anderen gleicht. Hier sind einige Beispiele, wie man diese Basistechniken einsetzen kann:
1. Drei aufeinanderfolgende identische Buchstaben vermeiden
Die meisten Binoxxo-Rätsel beginnen mit einigen vorgegebenen XX- und OO-Pärchen an verschiedenen Stellen. Da nicht mehr als zwei aufeinanderfolgende X oder O erlaubt sind, können wir also direkt auf beiden Seiten den jeweils anderen Buchstaben daneben platzieren, wie das Beispiel unten zeigt.
2. Drei aufeinanderfolgende identische Buchstaben vermeiden
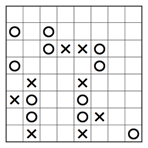
Eine andere häufige Situation ist X_X and O_O, wo zwei gleiche Buchstaben durch ein leeres Kästchen getrennt sind. Auch hier können wir direkt den jeweils anderen Buchstaben in das Kästchen in der Mitte eintragen, um drei aufeinanderfolgende identische Buchstaben zu vermeiden, wie im Beispiel unten gezeigt wird.
3. Drei aufeinanderfolgende identische Buchstaben vermeiden
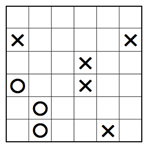
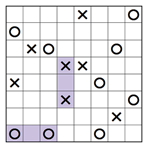
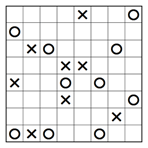
Manchmal kann ein X oder O nicht in einem Kästchen platziert werden, weil es ein oder zwei Schritte später eine verbotene Dreierkombination verursachen würde. Schauen wir uns Reihe 6 des teilweise gelösten Rätsels unten an. Wenn wir ein X in das linke Kästchen setzen, dann müssen die beiden anderen leeren Kästchen jeweils ein O enthalten, gemäss der Regel, dass jede Reihe oder Spalte die gleiche Anzahl X und O enthalten muss.
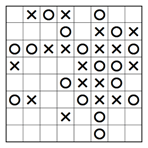
4. Eine Reihe oder Spalte vervollständigen
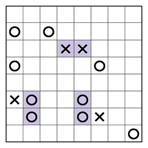
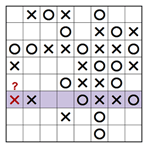
Gemäss der zweiten Regel muss die Anzahl an X und O in jeder Reihe oder Spalte gleich sein. Das bedeutet, dass in einem 8×8-Rätsel jede Reihe oder Spalte vier X und vier O enthalten sollte. Wenn wir uns nun die eingefärbte Reihe des teilweise gelösten Rätsels unten anschauen, sehen wir vier X und nur drei O, also muss in das leere Kästchen ein O gesetzt werden.
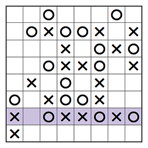
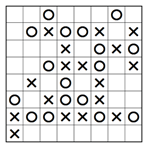
5. Zwei identische Reihen oder Spalten verhindern
Die dritte Regel von Binoxxo sagt, dass keine zwei Reihen oder Spalten identisch sein dürfen. In dem teilweise gelösten Rätsel unten sehen wir zwei eingefärbten Spalten, eine vollständige und eine mit zwei leeren Kästchen. Da in der unvollständigen Spalte ein X und ein O fehlen, gibt es nur eine Möglichkeit, sie zu platzieren, ohne eine zweite identische Reihe zu schaffen. Wie, zeigt das zweite Bild unten.
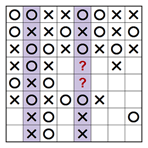
Fortgeschrittene Techniken
Die bis hierher beschriebenen Techniken reichen nicht aus, um schwierige Rätsel zu lösen. Für diese benötigen Sie Grips und fortgeschrittene Techniken, um viele spezielle und interessante logische Situationen herauszuarbeiten. Fortgeschrittene Techniken basieren auf einem Prozess von Vermutung und Konflikt, bei dem man bei einem Kästchen annimmt, dass es ein X (oder O) enthält, und sich diese Vermutung im nächsten Schritt durch reines logisches Kombinieren als falsch herausstellt. Hier sind einige Beispiele für fortgeschrittene Techniken, um spezielle Situationen zu lösen. Sie werden selbst noch viele weitere entwickeln, wenn Sie ein Binoxxo-Rätsel selber lösen:
1. Fortgeschrittene Technik
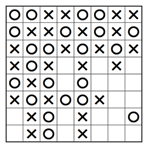
Schauen wir uns die eingefärbte Spalte im teilweise gelösten Rätsel unten an. Wenn wir ein O in das zweite Kästchen von oben setzen, dann haben wir vier der fünf O in dieser Spalte platziert. Das heisst also, dass noch ein O fehlt. Allerdings führt jedes Kästchen, in dem wir es versuchen, zu XXX an einigen Stellen. Das bedeutet, dass das zweite Kästchen von oben ein X enthalten muss, wie das rechte Beispiel unten zeigt.
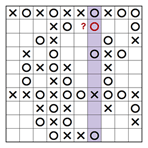
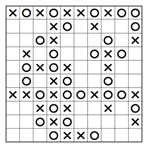
2. Fortgeschrittene Technik
Manchmal sind fortgeschrittene Techniken nötig, um zu verhindern, dass zwei identische Reihen oder Spalten entstehen. In dem teilweise gelösten Rätsel unten sehen wir zwei eingefärbte Spalten, eine vollständig und die andere mit drei leeren Kästchen. Schauen wir mal, was passiert, wenn wir ein O in das zweite Kästchen von unten setzen. Weil sich in dieser Spalte schon vier O befinden, müssten wir in den zwei leeren Kästchen jeweils ein X platzieren, um die gleiche Anzahl an X und O zu erhalten. Das würde allerdings zu zwei identischen Spalten führen, was gemäss den Regeln nicht erlaubt ist. Aus diesem Grund muss das zweite Kästchen von unten ein X enthalten.